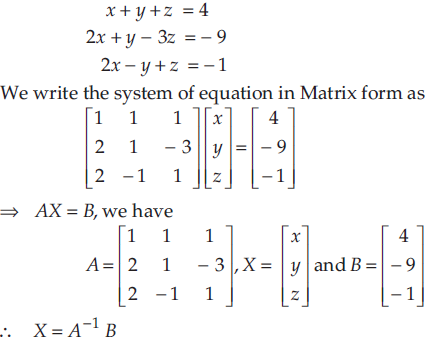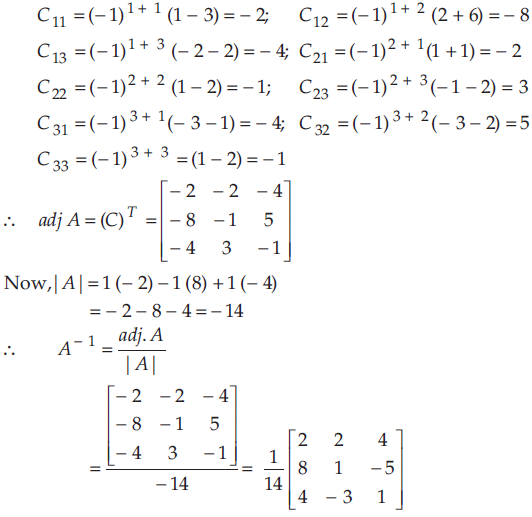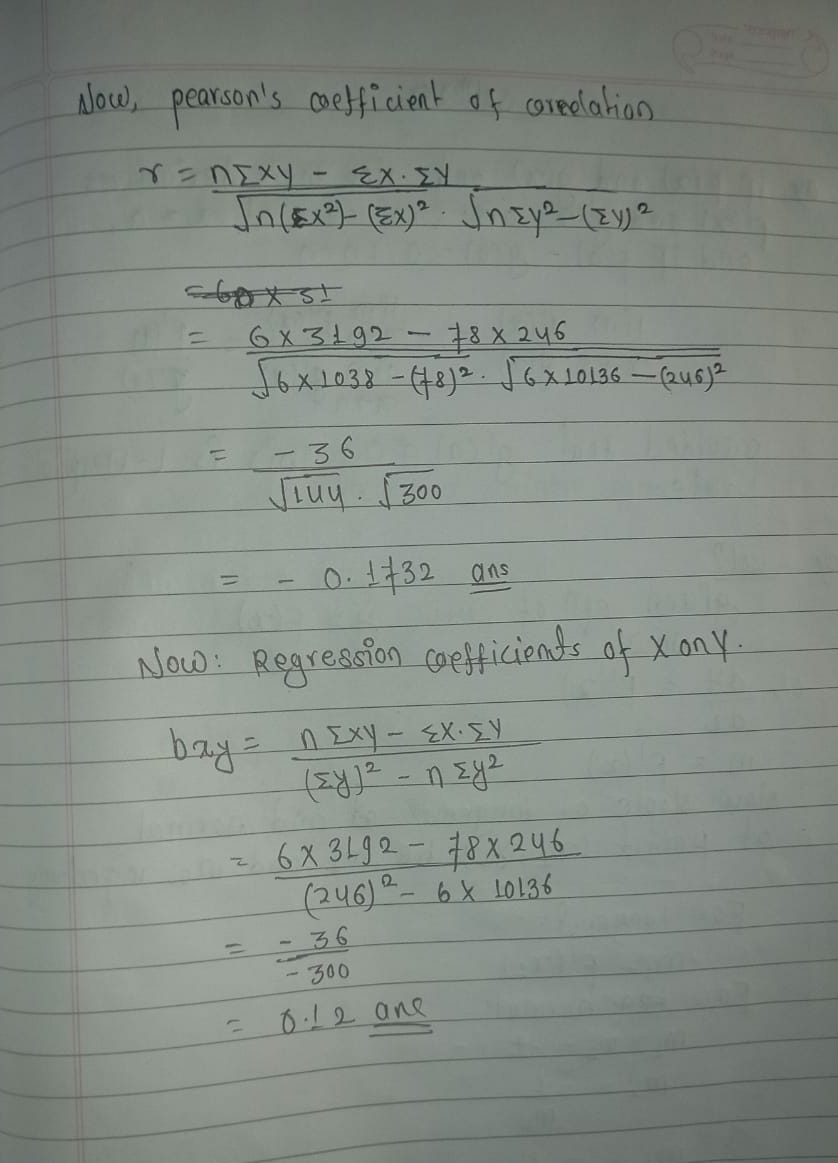NEB Class 12 Math Model Question 2080 With Solution

NEB Class 12 Math Model Question Paper 2079 With Solution 

---

In This Post, We Provide Complete Class 12 Mathematics [0041] Model Question and Answer Solution 2080 issued by NEB.

Check: SEE Math Model 2080 Solution (with grid)

Class 12 Model Question 2079

Class 12 Mathematics Model Questions 2079/80 With Solution. Latest NEB Model Question & Complete Answer Solution of Math for Class 12 Board Exam 2080. NEB Class 12 Model Question 2079/80 is given as:

Check: Latest Model NEB Class 12 Mathematics Model PDF 2080-2081

---

Class 12 Model Question Solution 2079

NEB Class 12 Model Question Solution 2079/80 is given as:

Disclaimer:
Answers mentioned here are not solved by teachers. These are the solutions written by a student of Grade 12. If you found some of the solutions mistake please let me know in the comment section below. I took help of book, search engines, and teachers to solve the set. However, the language or process of solving the questions might be informal and in examinations, you might have to add little more language and show more calculations than what has been done here. So, I highly encourage you to view these solutions as guide rather than just copying everything mentioned here.

Candidates are required to give their answers in their own words as far as practicable. The figures in the margin indicate full marks.

Time: 3hrs                                                                  Full Mark:75                                                                                                             

Attempt all questions.

Group "A"

1) What is an arrangement of the n natural numbers called?

• A) Induction
• B) Permutation
• C) Combination
• D) Expectation

Ans: B) Permutation

2) Let 1,w,w² be the cube roots of unity. Under which operation is the set A={1,w,w²} closed?

• A) Addition
• B) Subtraction
• C) Multiplication
• D) Division

Ans: C) Multiplication

3) What is the domain of sin^-1x?

• A) x≥1 or x≤-1
• B) (∞,infinity)
• C) -1<x<1
• D) -1≤x≤1

Ans: D) -1≤x≤1

4) ABCD is a parallelogram. Which one of the following represents area of the parallelogram?

• A) Magnitude of vector product of two vectors along AB and BD.
• B) Magnitude of vector product of two vectors along AB and DC.
• C) Magnitude of vector product of two vectors along AC and BC.
• D) Magnitude of vector product of two vectors along AB and AD.

Ans: A) Magnitude of vector product of two vectors along AB and BD.

5) If a conic section has eccentricity(e) = (√a^2-b^2)/a, what is the equation of that conic section?

• A)(x^2/a^2)-(y^2/b^2)=1
• B) (x^2/a^2)+(y^2/b^2)=1
• C) (x^2/a^2)+(y^2/a^2)=1
• D)(x^2/b^2)+(y^2/b^2)=1

Ans: B) (x^2/a^2)+(y^2/b^2)=1

6) If cosӨ =−1/2 for integer (n), what is the general value of Ө ?

• A) 2nπ ±2π/3
  
• B) nπ + (−1)^n π/3
  
• C) nπ −π/3
  
• D) nπ +π/3

Ans: A) 2nπ ±2π/3

7) Let A and B be two dependent events. If P (A) =1/2, P (B) = 3/4 and P(AnB) =2/5, what is the value of P(A/B)?

• A) equal to P(B/A)
• B) equal to P(A)
• C) less than P(A A B)
• D) less than P(B/A)

Ans:D) Less than P(B/A)

8) The edge of a cube increases from 10 cm to 10.025 cm. What would be the approximate increment in volume?

• A) 103 cm^3?
• B) 10.0253 cm^3?
• C) 7.5187 cm^3?
• D) 7.5 cm^3?

Ans: D) 7.5 cm^3?

9) What is the integrating factor of the differential equation cos'× dy + y =1°

• A) tan x
• B) e^tanx
• C) sec^2 x
• D)e^sec1x

Ans: B) e^tanx

10) What is the number of solutions of the system of linear equations × + y = 5 and x + y = 7?

• A) One solution
• B) No solution
• C) Infinite solutions
• D) More than one solution

Ans: B) No solution

11) Forces P and Q are acting along ceiling and floor of a rectangular room. What is the nature of the forces?

• A) Like
• B) unlike
• C) collinear
• D) parallel

Ans: B) unlike

Group "B"

12) For any positive integer n, (a+x)ⁿ = C₀aⁿ + C₁a^n-1x + C₂a^n-2x²+……+c_nxⁿ.

a) How many terms are there in the expression?

b) Write binomial coefficient in the expansions?

c) Write the general term of the expansion.

d) Write the relations among C (n, r-1), C (n+1, r) and C (n, r).

e) What is the value of C₀+C₁+C₂ +…+C_n?

Solution:

(a) There will be (n+1) numbers of terms in the expansion of (a+x)ⁿ = C₀aⁿ + C₁a^n-1x + C₂a^n-2x²+……+c_nxⁿ.

(b) The binomial coefficient in the expansion of (a+x)ⁿ = C₀aⁿ + C₁a^n-1x + C₂a^n-2x²+……+c_nxⁿ are: C₀, C₁a^n-1, C₂a^n-2,……C_n

(c) The general terms of the expansion is ⁿC_ra^n-rx^r.

(d) The relations among C (n, r-1), C (n+1, r) and C (n, r) is ⁿC­_r + ⁿC_r-1 = ⁿ⁺¹C_r.

(e) The value of C₀+C₁+C₂ +…+C_n is 2ⁿ.

13) a) Using the principle of mathematical induction, show that: 1+2+3+…+n < $\frac{1}{8}$(2n+1)².

b) Find the quadratic equation whose one of the cube roots is 2+$\sqrt{3}$

Solution:

Step 1: Let n = 1

P(1): 1<$\frac{1}{8}$[2(1)+1]² is true.

Hence, the statement is true for n=1

Step 2: Assume that the statement is true for n=k

P (k) : 1 + 2 + 3 + … + k < $\frac{1}{8}$ (2k+1)²

Step 3: Prove that the statement is true for n=k+1

We need to prove that:

1 + 2 + 3 + …. + (k+1) < $\frac{1}{8}$ [(2k+1)²] + k+1

< $\frac{1}{8}$ [4k²+4k+1] + 8 ×$\frac{1}{8}$ × (k+1)

<$\frac{1}{8}$ [4k²+4k+1+8k+8]

<$\frac{1}{8}$ [4k²+12k+9]

<$\frac{1}{8}$ [2k+3]²

<$\frac{1}{8}$[2(k+1)+1]²

(b) For the quadratic equation if one root (α)= 2 +$\sqrt{3}$

Another Root (β) = 2 - $\sqrt{3}$

Sum of Roots (α+ β) = 2 - $\sqrt{3}$ + 2 +$\sqrt{3}$ =4

Products of Roots (α × β) = (2 - $\sqrt{3}$)(2 + $\sqrt{3}$) = 1

∴Quadratic equation : x² -(α+ β)x + (α × β) =0

∴ x²−4x+1=0 is required equations.

14) a) Given y = sin^-1x and y>0, express cos y and tan y in terms of x.

b) If $\overrightarrow{a}$, $\overrightarrow{b}$, and $\overrightarrow{c}$ are any three vectors such that $\overrightarrow{a}$ × $\overrightarrow{b}$ = $\overrightarrow{a}$ × $\overrightarrow{c}$ for $\overrightarrow{a}$ ≠(0,0). Show that: $\overrightarrow{b}$ = $\overrightarrow{c}$.

 Solution:

(a) Given:

y = sin^-1x

or, x = sin y

We have, Cos²y + Sin²y = 1

Or, Cos²y=1- Sin²y

Or, Cos²y = 1-x²

Thus, Cos y = $\sqrt{1-x^2}$

And, $\mathrm{Tan}y=\frac{\sin x}{\cos x}=\frac{x}{\sqrt{1-x^2}}$

(b) Given:

$\overrightarrow{a}$ × $\overrightarrow{b}$ = $\overrightarrow{a}$ × $\overrightarrow{c}$

If Cross product is equal then their magnitude is also equal.

|$\overrightarrow{a}$ × $\overrightarrow{b}$ | = | $\overrightarrow{a}$ × $\overrightarrow{c}$|

Or, |$\overrightarrow{a}$|  |$\overrightarrow{b}$| Sinθ = | $\overrightarrow{a}$| |$\overrightarrow{c}$| Sinθ

Or, |$\overrightarrow{b}$ |=|$\overrightarrow{c}$ |

∴ $\overrightarrow{b}$ = $\overrightarrow{c}$

15) The price in Rupees (X) and demand in unit (Y) of 6 days of a week is given as:

X	10	12	13	12	16	15
Y	40	38	43	45	37	43

Calculate the Pearson’s Coefficient of Correlation and the regression coefficients of X on Y.

 Solution:

x	y	xy	x2	y2
10	40	400	100	1600
12	38	456	144	1444
13	43	559	169	1849
12	45	540	144	2025
16	37	592	256	1369
15	43	645	225	1849
Σx=78	Σy=246	Σxy=3192	Σx2=1038	Σy2=10136

Value of n = 6

$$r=n∑xy−∑x∑yn∑x2−(∑x)2.n∑y2−(∑y)2

$$r=6×3192−78×2466×1038−(78)2.6×10136−(246)2

$$r=−0.36144.300

$$r=−1.7132

Now, Regression Coefficient of x on y is

$$bxy=n∑xy−∑x∑y(∑y)2−n∑y2

$$bxy=6×3192−78×2462462−6×10136

$$bxy=−36−300

$$∴bxy=0.12

16) a) Define Hospital’s rule.

b) Write the slope of the tangent and normal to the curve y =f(x) at (x₁,y₁).

c) Write the integral of $\int \frac{1}{x^2+a^2}dx$.

d)What is the integral of $\int \sinh x.dx$

Solution:

(a) If f(x) and g(s) are two function then their derivatives f’(x) and g’(x) are continuous at x=0 and if f(a) =g(a), then,

$\underset{x\to a}{lim}\frac{f(x)}{g(x)}=\underset{x\to a}{lim}\frac{f^{\prime }(x)}{g^{\prime }(x)}=\frac{f^{\prime }(a)}{g^{\prime }(a)}$ When g’(a)≠0.

(b) The slope of tangant to the curve y=f(x) at (x₁,y₁) is

$$dydx=f′(x)

$$⇒dydx(x1,y1)=f′(x1)

Then, Slope of normal to y=f(x) at ((x₁,y₁)) is

F’(x). m = -1

Thus, m=$-\frac{dx}{dy}$

(c) $\int \frac{1}{x^2+a^2}dx$=$\frac{1}{a}{\tan }^{-1}\frac{x}{a}+C$

(d) $\int \sinh x.dx$ = coshx +C

17) a) Solve: $\frac{dy}{dx}=\frac{y}{x}$

b) Verify Rolle’s Theorem for f(x) = x²+3x-4 in [-4,1].

 Solution:

$$dydx=yx

$$dyy=dxx

Integrating both sides:

ln(y) = ln(x) +C

or, ln(y) = ln(x) + ln(C)

Thus, y=xc

(b) f(x) = x²+3x-4 in [-4,1]

(i) Here f(x) is a polynomial function so it is continuous at [-4,1].

(ii) f’(x) = 2x+3

f(x) is differentiable in (-4, 1).

(iii) f(-4) = 0, f(1) = 0

Thus, f(a) = f(b).

All the condition of Rolle’s Theorem are verified. So there exists at least a point C ε (-4, 1).

Such that: f’(C) =0.

18) Using simplex method, maximize P (x, y) = 15x+10y subject to 2x+y≤10, x+3y≤10, x, y≥0.

 Solution:

Maximize P (x, y) = 15x+10y

Subject to:

2x+y≤10

x+3y≤10

x, y≥0

Let S₁ and S₂ be two non-negative slack variables. Then, the standard form of the above LPP is:

2x+y+r =10

x+3y+s=10

-15x-10y+P=0

The initial simplex tableau for above LLP is

Basic Variable	x	y	r	s	p	Constant
r	2	1	1	0	0	10
s	1	3	0	1	0	10
	-15	-10	0	0	1	0

In the initial Simplex tableau the most negative entry is -15 so the x-column is pivot column. Also, $\frac{10}{2}$=5 is the smallest positive value. Thus, r-row with element 2 on x column is the pivot element.

Dividing First Row by 2

Basic Variable	x	y	r	s	p	Constant
r	1	½	½	0	0	5
s	1	3	0	1	0	10
	-15	-10	0	0	1	0

R₂à R₂-R₁ and R₃à R₃+15R₁

Basic Variable	x	y	r	s	p	Constant
r	1	½	½	0	0	5
s	0	$\frac{5}{2}$	-½	1	0	5
	0	-$\frac{5}{2}$	$\frac{}{}$152	0	1	75

Here last row still has -ve entry. So y is pivot column and s-row is the pivot row with $\frac{5}{2}$ as pvot element.

R₂à $\frac{2}{5}$R₂

Basic Variable	x	y	r	s	p	Constant
r	1	½	½	0	0	5
s	0	1	-$\frac{1}{5}$	$\frac{}{}$25	0	2
	0	-$\frac{5}{2}$	$\frac{}{}$152	0	1	75

Again, R₃ à R₃+$\frac{5}{2}$R₂ and R₁àR₁- ½ R₂

Basic Variable	x	y	r	s	p	Constant
r	1	½	$\frac{3}{5}$	-$\frac{1}{5}$	0	4
s	0	1	-$\frac{1}{5}$	$\frac{}{}$25	0	2
	0	0	7	1	1	80

Since there is no negative entry in last row. Thus Maximum Solution is obtained.

P_max=80 at x=4 and y=2.

19) A particle is projected with a velocity ‘v’ and greatest height is ‘H’, prove the horizontal range R is: R = 4$\sqrt{H\left(\frac{v^2}{2g}-H\right)}$.

Solution:

Let β be angle of projection. Then,

$$H=v2sin2β2g

$$R=v2sin⁡2βg

Now,

$$v22g−H

=$\frac{v^2}{2g}-\frac{v^2{\sin }^2\beta }{2g}$

=$\frac{v^2}{2g}(1-{\sin }^2\beta )$

=$\frac{v^2}{2g}{\cos }^2\beta$

And,

R.H.S of Question:

4$\sqrt{H\left(\frac{v^2}{2g}-H\right)}$ = $4.\frac{v\sin \beta .\cos \beta }{2g}$

$$4v2sin2β2g.v22gcos2β

$$4.v2sin⁡β.cos⁡β2g

$\frac{}{}$v2.2sin⁡β.cos⁡βg

$\frac{}{}$v2sin⁡2βg

=R

=L.H.S

OR

The cost function C(x) in thousands of rupees for producing x units of math’s textbooks is given by C(x)=30+20x-0.5x² , 0≤x≤15.

a) Find the marginal cost of Function.

b) Find the marginal cost for producing 12000 math’s textbooks.

 Solution:

C(x)=30+20x-0.5x², x, y≥0

(a) Marginal Cost of Function = C‘(x)=0+20-x

(b) Marginal cost = 20-x=20-12=Rs. 8 (in thousands)

Group "C"

20) a) Using matrix methods, solve the following system of linear equations: x+y+z = 4, 2x+y-3z = -9,2x-y+z = -1

b) Apply De-Moiver’s theorem to find the value of [2(𝑐𝑜𝑠15° + 𝑖𝑠𝑖𝑛15°)] ⁶

c) Prove that: $\left(1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+...\right)\left(1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+...\right)=1$

 Solution:

(a)

(b) De Moiver’s Theorem states that, {r(cosθ+isinθ)}ⁿ=rⁿ(cosnθ+isinnθ).

∴[2(𝑐𝑜𝑠15° + 𝑖𝑠𝑖𝑛15°)] ⁶ = 2⁶ [cos90 + i sin90] = 64i

(c) We Know  e^x=  $1+\frac{x}{1!}+\frac{x^2}{2!}+\frac{x^3}{3!}+...$

Put x = 1

e¹=$1+\frac{1}{1!}+\frac{1}{2!}+\frac{1}{3!}+...$(i)

Put x = -1

e^-1=$1-\frac{1}{1!}+\frac{1}{2!}-\frac{1}{3!}+...$(ii)

Taking LHS of Question:

$$(1+11!+12!+13!+...)(1−11!+12!−13!+...)

=e × e^-

=1

=R.H.S

21) a) Find the direction cosines of the line joining the points (4,4,-10) and (-2,2,4).

b) Find the angle between the two diagonals of a cube.

c) Find the vertices of the conic section: 16(y-1)² -9(x-5)² = 144.

 Solution:

(a) Given Points: P(4,4,-10) and Q(-2,2,4)

Direction ratios of PQ = -2-4, 2-4, 4-(-10)=-6, -2, 14

PQ=$\sqrt{{(-6)}^2+{(-2)}^2+{(14)}^2}=2\sqrt{59}$

Thus, Direction cosines are: $\frac{-6}{2\sqrt{59}},\frac{-2}{2\sqrt{59}},\frac{14}{2\sqrt{59}}$

(b) Let OABCDEFG be a cube with vertices as below 

O(0,0,0),A(a,0,0),B(a,a,0),C(0,a,0),D(0,a,a),E(0,0,a),F(a,0,a),G(a,a,a)

There are four diagonals OG,CF,AD  and BE for the cube.

Let us consider any two say OG and AD

We know that if A(x1​,y1​,z1​) and B(x2​,y2​,z2​) are two points in space then

AB=(x₂​−x₁​)i+(y₂​−y₁​)j+(z₂​−z₁​)k

⇒OG=(a−0)i+(a−0)j+(a−0)k=ai+aj+ak

and AD=(0−a)i+(a−0)j+(a−0)k=−ai+aj+ak.

Therefore ∣$\overrightarrow{OG}$∣=$\sqrt{a^2+a^2+a^2}=a\sqrt{3}$

And,

$\overrightarrow{AD}$ = $\sqrt{{(-a)}^2+a^2+a^2}=a\sqrt{3}$

$$OG→.AD→=−a2+a2+a2=a2

We know that angle between two vectors $\overrightarrow{OG},\overrightarrow{AD}$ is given by θ = ${\cos }^{-1}\frac{\overrightarrow{OG}.\overrightarrow{AD}}{|\overrightarrow{OG}|.|\overrightarrow{AD}|}$

=${\cos }^{-1}\frac{a^2}{a\sqrt{3}.a\sqrt{3}}$

=${\cos }^{-1}\frac{1}{3}$

Thus, angle between two vectors $\overrightarrow{OG},\overrightarrow{AD}$ is ${\cos }^{-1}\frac{1}{3}$

(c) Given:

16(y-1)² -9(x-5)² = 144….(i)

Dividing Both Sides by 144.

$$(y−1)29−(x−5)216=1

Comparing with $\frac{{\left(y-h\right)}^2}{a^2}-\frac{{\left(x-k\right)}^2}{b^2}=1$

We Get:

h=1, k=5, a=3, b=4

Thus, Vertex = (h±a, k) = (1±3, 4) =(4,4) 0r (-2, 4)

22) a) If the limiting value of $\frac{f(x)-5}{x-3}$ at x= 3 is 2 by using L’ Hospital’ rule, find the appropriate value of f(x).

b) Write any one homogeneous differential equation in (x,y) and solve it.

c) The concept of anti-derivative is necessary for solving a differential equation. Justify this statement with example.

 Solution:

(a)$\begin{array}{l}\frac{\underset{x\to 3}{lim}f(x)-5}{x-3}=2\\ or,\underset{x\to 3}{lim}f(x)-5=2x-6\\ or,\underset{x\to 3}{lim}f(x)=2x-1\end{array}$

(b)  Homogenous differential Equation in (x,y) is $\frac{dy}{dx}=\frac{y}{x}+1$

Solving This Equation:

$$dydx=yx+1

Put y =vx, then $\frac{dy}{dx}=v+x\frac{dv}{dx}$

$\begin{array}{}\end{array}$yx+1=v+xdvdxor,v+1=v+xdvdxor,1=xdvdxor,dxx=dv

Integrate both sides

v = log x + log c

or, v = log cx

Replacing v

$$yx=log⁡cx

∴ y = x log cx 

(c) The concept of anti-derivatives is necessary for solving differential equation. Let’s understand this statement through the following example:

Consider a differential Equation $\frac{dy}{dx}=\frac{x}{y}$

i.e., y.dy = x.dx

Let’s integrate this on both sides:

$$∫y.dy=∫x.dx

$$y22=x22+C

Or, y²=x²+2C

i.e., y²=x²+C

---

Math Model Question Solution Youtube Video

---

The below answer provided for question 15 is incorrect. you can check correct answer from above but 

Formula n€y²-(€y)2 hunxa formula

ans -0.12 aau xa.

Group "C"

---

Download Math Model Question Solution

Download

---

• NEB Class 12 Model Question 2079/80 | All Subjects

• NEB Class 12 Physics Model Question Paper 2079 With Solution

• NEB Class 12 Computer Model Question Paper 2079 With Solution

---